Speciality -Mechanical and Aerospace engineering-

Theoretical and practical application skills

After graduation from Tokyo Institute of Technology in mechanical engineering in bachelor, I study aerospace engineering at the University of Stuttgart, Germany. I major in numerical simulations and control engineering.

Application of mechanical and control engineering

Fully automatic Beerserver

Tokyo Institute of Technology, where I completed my bachelor's degree, has a "Development Project" in the mechanical engineering department. This is a voluntaly course in which each group sets its own task based on a given theme and builds a robot within a budget of 100,000 Yen(800 Euro) and a very well equiped work environment.

The theme at the time was "a recreational robot" and our group built a fully automatic beer server that can even open a can. We were able to grasp the overview of the whole field and the flow of a development by designing and building the robot with all the knowledge of various mechanics, electric circuits and programming, which we had studied individually until then.

Flight Control System using Reinforcement Learning

I am studying aerospace engineering at the University of Stuttgart, Germany, specializing in experiment and numerical computation and control engineering. With the recent rise of machine learning in the information field, its applications have been studied in aerospace engineering and fluid dynamics too. A flight control using machine learning was conducted as a student project at this university.

The objective of this project using reinforcement learning was to make the aircraft fly through green transit points while avoiding black obstacles. High- and Low-level control inputs are tested to develop the model.

Although only small obective was accomplished due to the lack of computer resources due to the corona, it was a good experimece to understand the advantages and problems of reinforcement learning. I am also using this experience to work as a research assistant for optimization problems using reinforcement learning at the university.

Implementation of Flight Control System using Feedback Loops

In the aviation field, reliability is the biggest requirement. Machine learning is characterized by its wide range of applications, but it has the problem that reliability cannot be guaranteed, and therefore, careful consideration is required when applying it to the field of aviation. On the other hand, conventional control techniques can guarantee their reliability mathematically in many cases. It is required to consider the advantages and disadvantages of each of them and to adopt an appropriate technique according to the situation.

In universities, students study classical control techniques such as control loops using transfer functions, modern control using equations of state, and the theory of optimization problems. However, if we design without these theories, we cannot adopt appropriate methods according to the risk and cost, and this may results in serious error or many deaths. Therefore, it is very important to learn them. In order to connect theory and practice, I conducted the verification of control loops that I have implemented in a model airplane.

Understanding of Fluid Simulation

Simulation is now highly needed in various development fields. However, simulation has various limitations, and the accuracy of the results strongly depends on the assumptions.

I learned the three main methods for numerical fluid simulation (Finite Difference Method (FDM), Finite Element Method (FEM) and Finite Volume Method (FVM)) at the University of Stuttgart and implemented them in practice for simple problems.

Finite Difference Method

The finite difference method is the simplest method and it is the basis for understanding more advanced numerical methods. I implemented a simulation of the temperature distribution from scrach when a hot fluid touches a cold metal plate. (Since it takes a very long time to reach steady state, the following Gif image was terminated before that.)

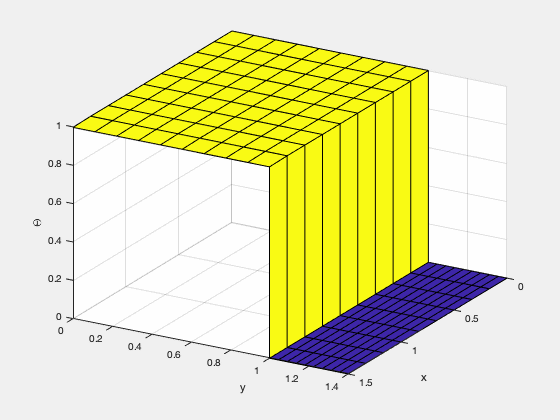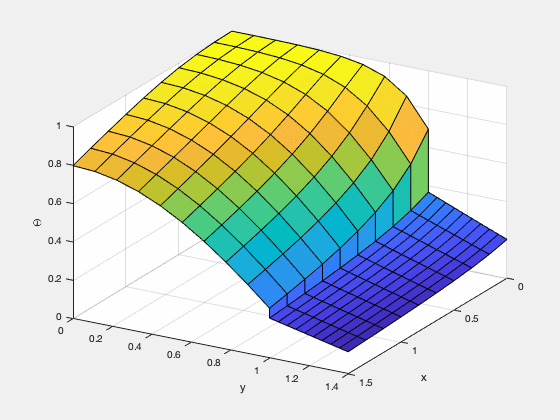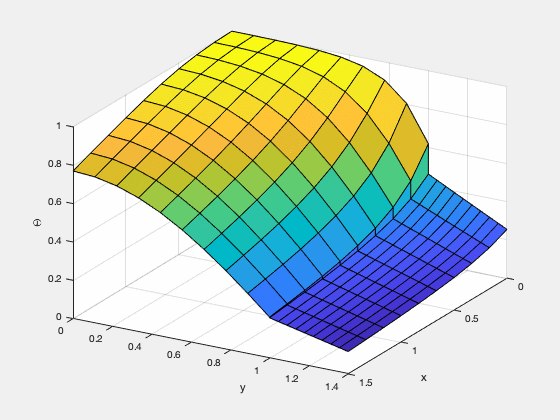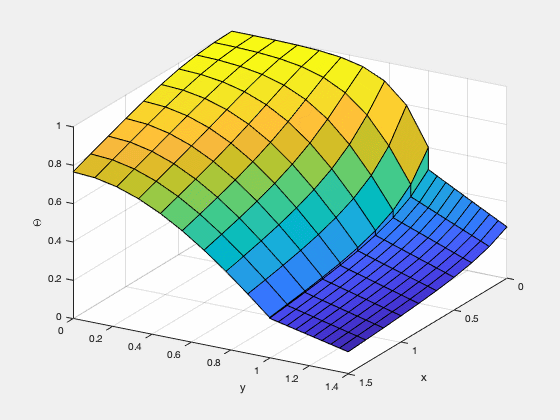
Finite Element Method

FEniCS is a finite element method framework developed by universities and institutes, which allows users to perform simulations by directly inputting governing equations and boundary conditions using the Python interface. The types of elements which can be used in the calculations are very diverse, and the a variety of methods can be selected according to the characteristics of the problem.

In the figure below, the distribution of substance C produced by the chemical reaction between two substances A and B is simulated.

　

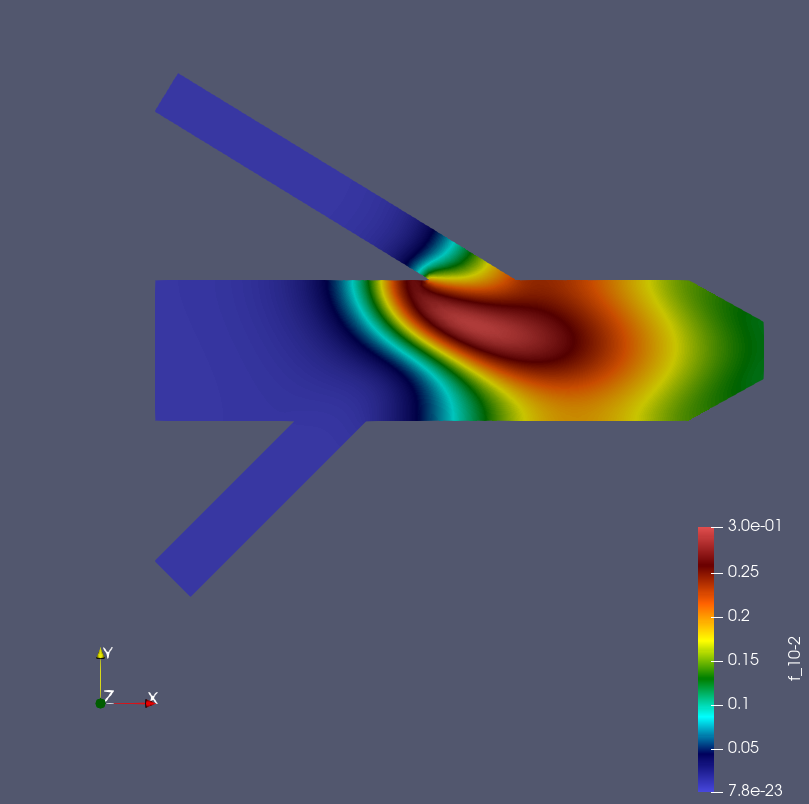
Finite Volume Method

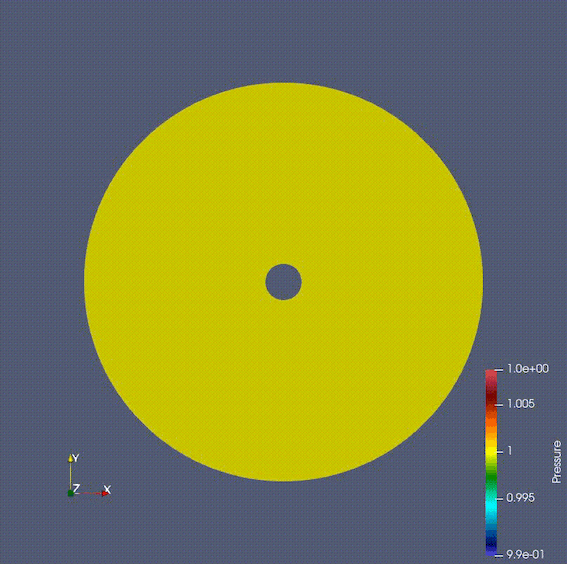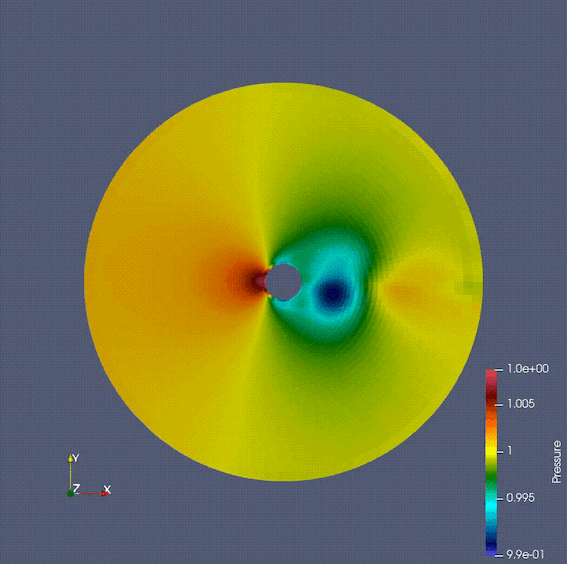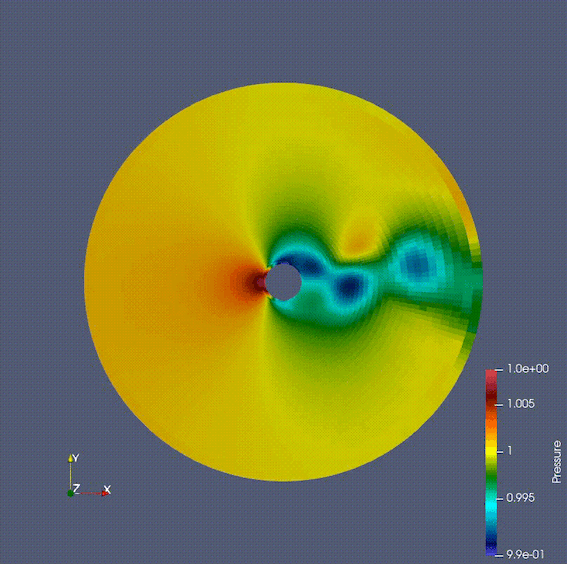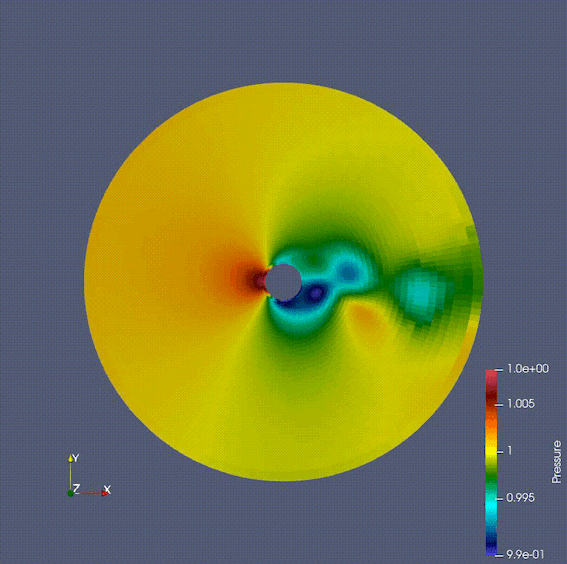
The finite volume method focuses on conserved quantities and can be applied to problems such as shock waves, which are difficult/impossible to calculate by the finite difference method and finite element method. Therefore, this method is used in many cases of numerical fluid dynamics simulations in the aerospace field. I have implemented various numerical flux calculation methods, boundary conditions, space and time discretization and solution methods in Fortran and understood their behaviors.

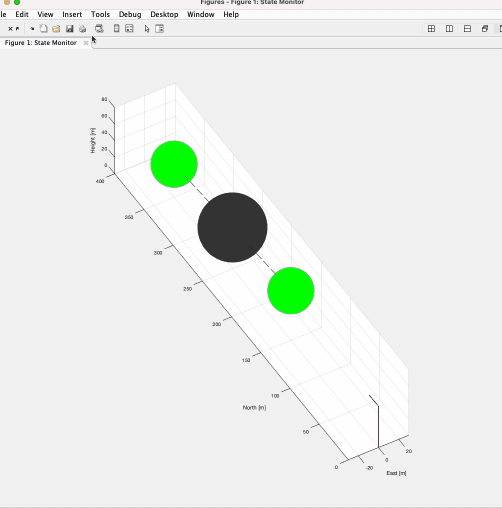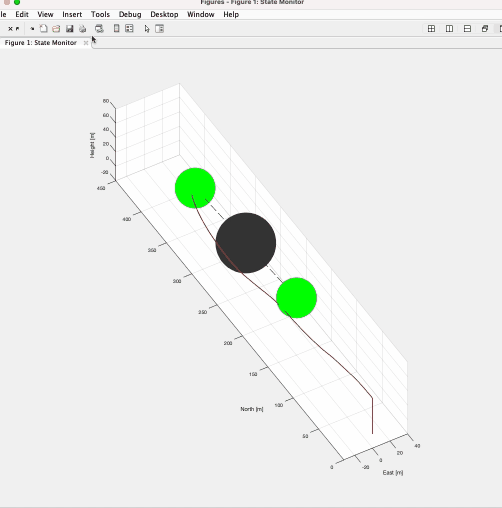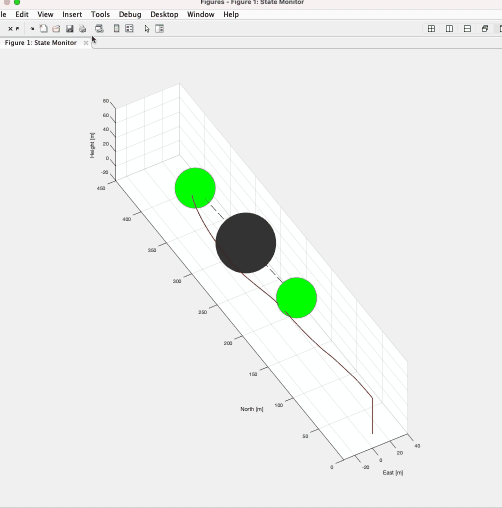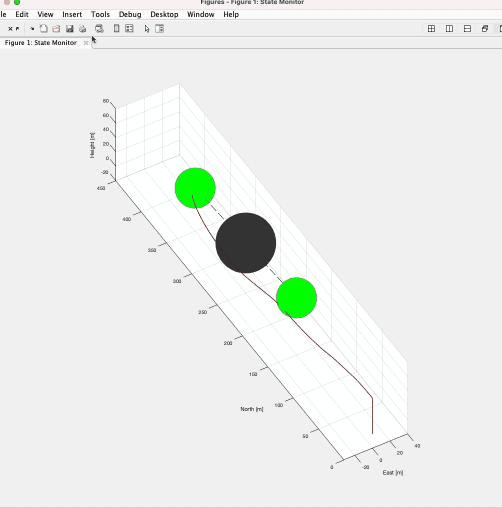
The Gif image below shows a fluid flowing around a cylinder, calculated using the Navier-Stokes equations. It can be seen that the Karman vortex is generated, which does not appear in the Stokes equation or the potential flow.